Previous Example Introduction Next Example

Example 13

Let G be the group generated by the two matrices below. Calculate the "graph of inclusions" for the geometric class given by G. 
3x3
 1  0  0
 1 -1  0
 0  0 -1
3x3
 -1 1 0
 -1 0 0
  0 0 1

Used Programs

Order, Graph

Solution

  1. Write the two matrices in a file 'G' and add 
      #g2
    as top row. Call 
       Order -o G >> G
    to get the group with the correct order in file 'G'.
  2. Call 
       Graph G
    to get the following output: 
    
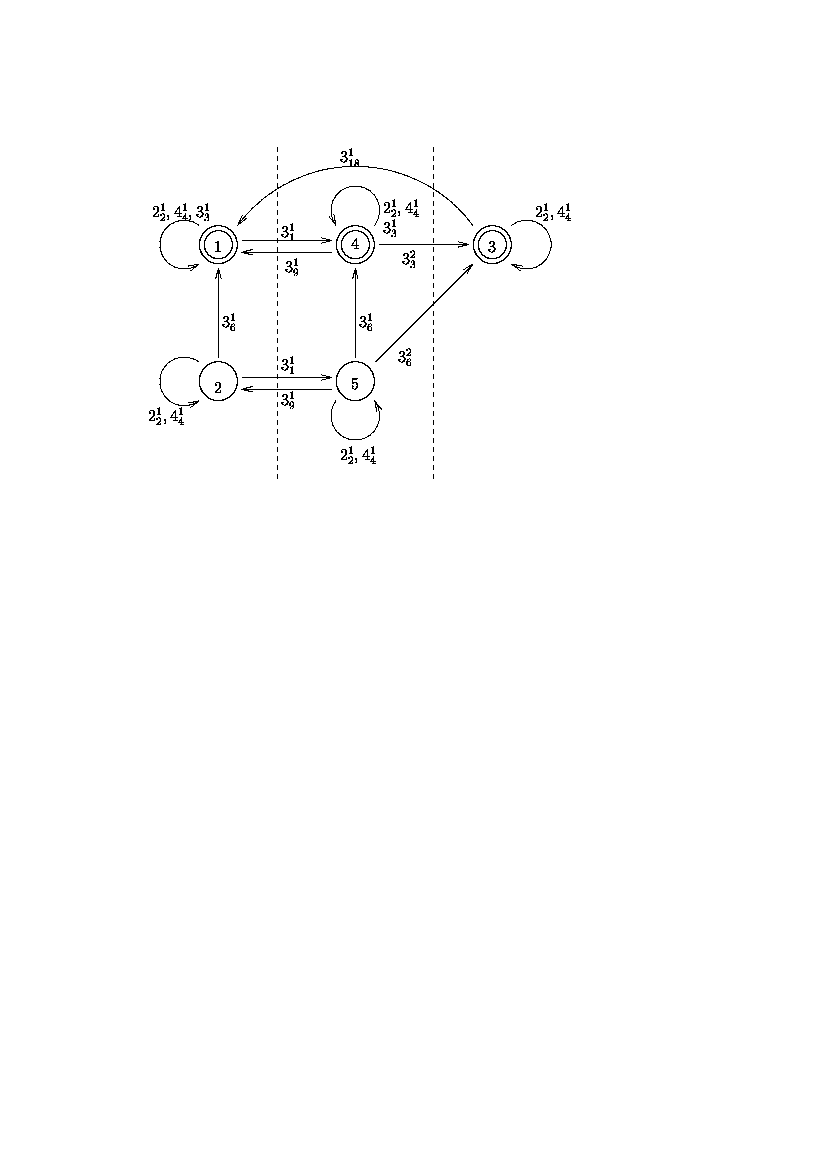
father: level 1 number of orbits 1 lengths 2
There are 3 Z-classes with 2 1 2 affine classes!
1: 1 (2, 1, 2^1)
1: 1 (4, 1, 2^2)
1: 1 (3, 1, 3^1)  2 (6, 1, 3^1)
2: 2 (2, 1, 2^1)
2: 2 (4, 1, 2^2)
1: 3 (18, 1, 3^1)
1: 4 (9, 1, 3^1)
2: 5 (9, 1, 3^1)
3: 3 (2, 1, 2^1)
3: 3 (4, 1, 2^2)
3: 4 (3, 2, 3^1)  5 (6, 2, 3^1)
4: 1 (1, 1, 3^1)
5: 2 (1, 1, 3^1)
4: 4 (2, 1, 2^1)
4: 4 (4, 1, 2^2)
4: 4 (3, 1, 3^1)  5 (6, 1, 3^1)
5: 5 (2, 1, 2^1)
5: 5 (4, 1, 2^2)
5
 3 1 1 1 0
 0 2 0 0 1
 0 0 2 1 1
 1 0 0 3 1
 0 1 0 0 2
    The program first gives the number of arithmetic/Z-classes in the geometric class and the number of affine classes in each arithmetic class.
    The affine classes are consecutively numbered. The first affine class of each arithmetic class consits of symmorphic space groups (affine classes 1,3 and 4).
    A row 
       s: r (u, o, i)  R (U, O, I)
    has the following meaning:
    There is an edge from the affine class r to the affine class s with label iuo and an edge form the affine class R to the affine class s with label IUO (i.e.: the index in the group-subgroup-relationship is I, the length of the orbit of the affine normalizer on the supergroups is O and the orbit of the affine normalizer on the subgroups has length U).
    The matrix shows the edges of the graph. The 3 in the forth line and the forth column means, that there are three edges from the affine class with number 4 to itself. The 1 in the forth row and the first column means, that there is one edge from the affine class with number 4 to the affine class with number 1.
  3. The following picture visualizes the graph (if there are several edges between two affine classes, only one is drawn with the labels of all of them):
    Visualisation of the graph
Previous Example Introduction Next Example